數據造假的(de)甄别在數據分(fēn)析領域是一個(gè)熱(rè)門的(de)話(huà)題，也(yě)是對(duì)數據分(fēn)析師的(de)一項挑戰。分(fēn)析數據造假的(de)方法有很多(duō)種。我們在前面的(de)系列文章(zhāng)中曾經介紹過兩種檢驗作弊流量的(de)方法。一種是根據曆史經驗及分(fēn)布情況的(de)多(duō)維度交叉檢驗，另一種是使用(yòng)随機森林(lín)模型根據已知作弊流量的(de)特征對(duì)新流量進行分(fēn)類及預測。

本篇文章(zhāng)介紹一種神奇的(de)數據檢驗方法，本福德定律(Benford's Law)。本福德定律是一種用(yòng)途廣泛的(de)數據檢驗方法，在安然公司破産和(hé)伊朗大(dà)選選票(piào)甄别中都曾被使用(yòng)到。本福德定律通(tōng)過自然生成的(de)數字中1到9的(de)使用(yòng)頻(pín)率對(duì)數據進行檢驗。如果你的(de)數據具備一定規模，沒有人(rén)工設定的(de)最大(dà)值和(hé)最小值，并且數據本身受人(rén)爲因素影(yǐng)響較小。那麽就可(kě)以使用(yòng)本福德定律對(duì)數據進行檢驗，甄别數據是否經過人(rén)爲修飾。

本福德定律及公式

本福德定律中自然生成的(de)數字首位爲1的(de)概率爲30.10%，2的(de)概率爲17.61%，依次遞減，首位爲9的(de)概率僅爲4.58%。依據這(zhè)一期望概率值我們可(kě)以對(duì)數據進行檢驗。以下(xià)是本福德定律的(de)計算(suàn)公式。通(tōng)過這(zhè)一公式可(kě)以計算(suàn)出1-9中每個(gè)數字出現數據首位的(de)概率。

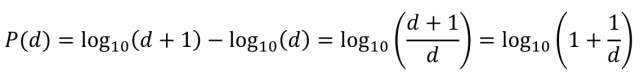
舉例來(lái)說，對(duì)于數字9下(xià)面的(de)公式可(kě)以計算(suàn)出一組自然生成的(de)數字中9出現在數字首位的(de)概率是多(duō)少。

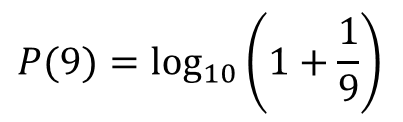
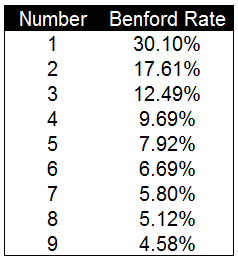
我們使用(yòng)本福德定律公式逐一計算(suàn)了(le)數字1-9出現在首位的(de)概率。以下(xià)是每個(gè)數字出現的(de)概率值。後面會根據這(zhè)一期望的(de)概率值對(duì)數據是否進行過人(rén)工修改進行甄别。

通(tōng)過圖表可(kě)以更較直觀的(de)看到本福德定律中每個(gè)數字出現的(de)頻(pín)率以及不同數字間的(de)差異。與我們想象的(de)不同，數字出現的(de)頻(pín)率并不是均勻分(fēn)布的(de)。1出現的(de)次數爲30.10%而9出現的(de)次數僅爲4.58%。

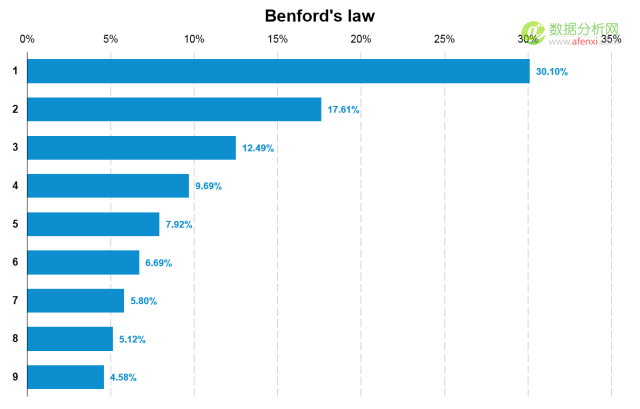下(xià)面我們将使用(yòng)本福德定律對(duì)工作中常見的(de)數據進行檢驗，甄别數據是否經過人(rén)爲修飾。

廣告展現量數據檢驗

首先檢驗一組廣告曝光(guāng)數據。下(xià)面是某廣告一段時(shí)間的(de)曝光(guāng)量數據。我們将每條展現量數據的(de)第一個(gè)數字提取出來(lái)，通(tōng)過本福德定律對(duì)這(zhè)組數據進行檢驗。

第一步計算(suàn)展現量數據中數字1-9出現的(de)次數。第二步計算(suàn)所有展現量數據的(de)條目，展現量數據爲474條。第三步計算(suàn)數字1-9出現次數的(de)頻(pín)率。第四步使用(yòng)本福德定律計算(suàn)出數字1-9出現頻(pín)率的(de)期望值。

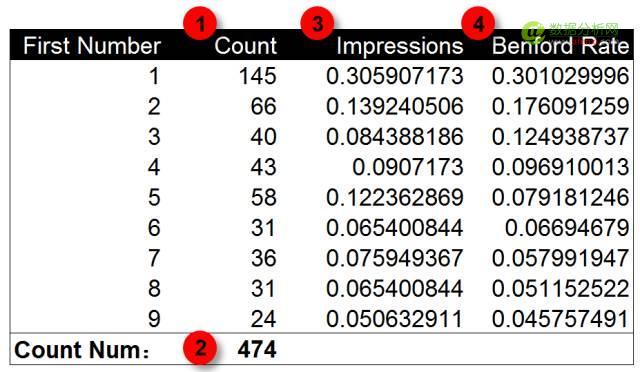
将曝光(guāng)量數據和(hé)本福德定律的(de)期望值繪制到圖表中進行對(duì)比，可(kě)以發現曝光(guāng)量數據首位數字出現的(de)頻(pín)率與本福德定律整體上基本一緻。在數字2，3和(hé)5上略有差異。這(zhè)個(gè)柱狀圖能說明(míng)什(shén)麽？表明(míng)數據符合本福德定律？三個(gè)數據點上的(de)差異又說明(míng)什(shén)麽？數據中存在人(rén)爲修飾嗎？

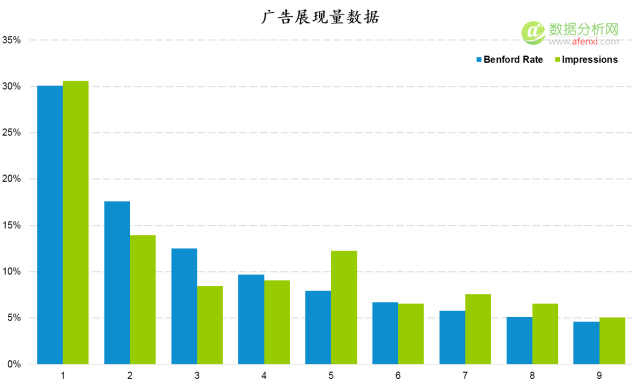
單從實際概覽值和(hé)圖表上我們無法辨别數據是否經過人(rén)爲修飾。要準确的(de)判斷數據是否爲自然生成還(hái)需要計算(suàn)兩個(gè)指标，分(fēn)别爲KS值和(hé)截止值。然後對(duì)兩個(gè)指标進行對(duì)比。如果KS值低于截止值，那麽可(kě)以判定數據爲自然生成，沒有經過人(rén)工修飾。否則就可(kě)能有造假的(de)風險。

KS值是數據的(de)實際概率值與期望概率值差異的(de)最大(dà)值，截止值是1.36除以數據條目數的(de)平方根。我們對(duì)前面的(de)數據表計算(suàn)KS值和(hé)截止值。第五步，計算(suàn)實際概率值與期望概率值的(de)差異。這(zhè)裏我們取差異的(de)絕對(duì)值以避免負數的(de)産生。第六步，計算(suàn)K-S值，經過計算(suàn)K-S值爲0.043，也(yě)就是數字5出現頻(pín)率的(de)差異。第七步，計算(suàn)截止值，這(zhè)裏的(de)曝光(guāng)數據共有474條，因此截止值爲0.053。第八步，對(duì)比K-S值與截止值，K-S值小于截止值。因此數據屬于自然生成。沒有經過人(rén)爲修飾。

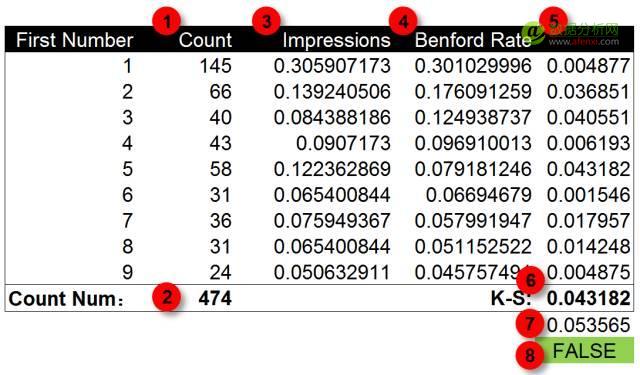
廣告點擊量數據檢驗

按照(zhào)前面的(de)方法，我們對(duì)同一組廣告的(de)點擊量數據進行檢驗。在下(xià)面的(de)柱狀圖中，藍色爲本福德定律的(de)期望概率值，綠(lǜ)色爲廣告點擊量的(de)首位數字分(fēn)布情況。可(kě)以發現在數字1,3和(hé)4上實際值與期望值之間存在較大(dà)的(de)差異。尤其是在數字3上。但僅根據這(zhè)幾個(gè)差異點我們還(hái)不能判斷數據是否經過人(rén)工修飾。

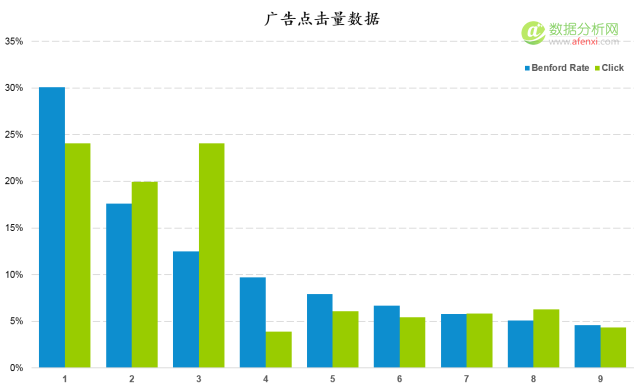
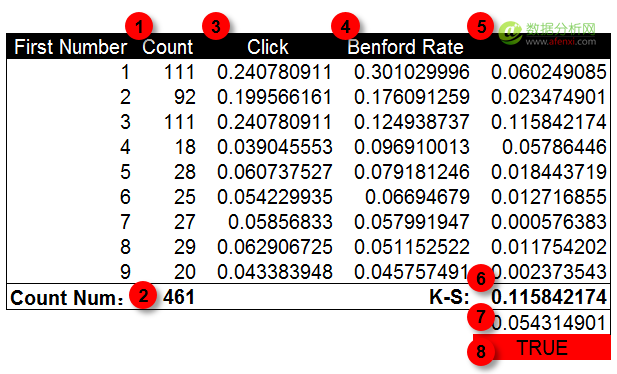
進一步計算(suàn)K-S值和(hé)截止值并進行對(duì)比。K-S值爲數據點間的(de)最大(dà)差異值，這(zhè)裏是0.115。截止值經過計算(suàn)爲0.054。K-S值明(míng)顯大(dà)于截止值。因此可(kě)以判斷點擊量數據是經過人(rén)工修飾的(de)可(kě)能，需要進一步進行檢驗。

貸款金額數據檢驗

除了(le)廣告數據以外，本福德定律還(hái)可(kě)以在很多(duō)場(chǎng)景下(xià)對(duì)數據進行檢驗。如貸款金額的(de)數據。下(xià)面是一組貸款金額首位數字分(fēn)布與本福德定律逾期分(fēn)布的(de)對(duì)比圖。兩者的(de)趨勢一緻，差異也(yě)較小。

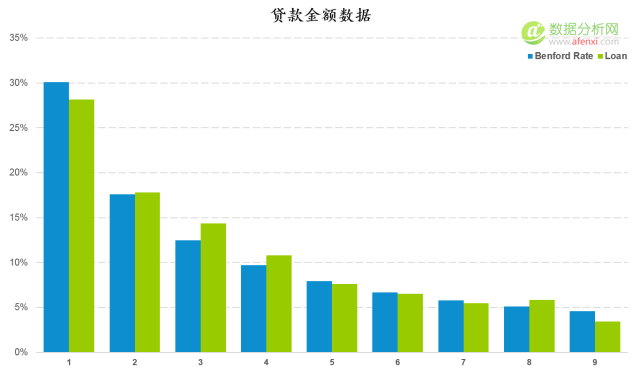
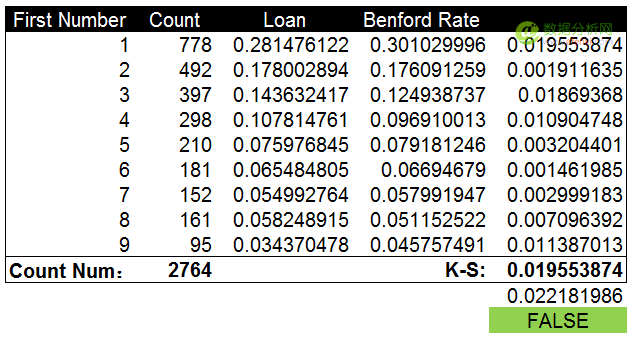
通(tōng)過計算(suàn)K-S值和(hé)截止值并進行對(duì)比，K-S值0.019小于截止值0.022。說明(míng)貸款金額數據爲自然生成，不存在人(rén)工修飾。

Excel随機數檢驗

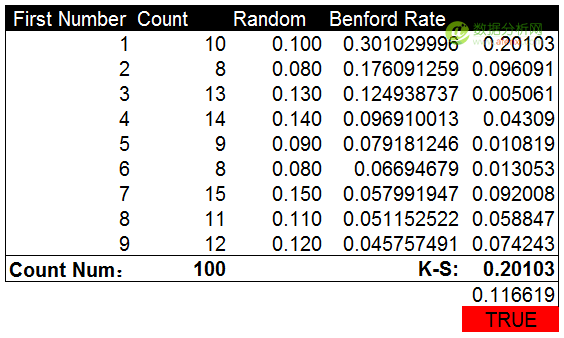
最後，我們人(rén)工生成一組”假數據”，看看本福德定律的(de)檢驗結果。這(zhè)裏使用(yòng)Excel的(de)随機數函數生成100個(gè)随機數。并與本福德定律的(de)期望分(fēn)布進行對(duì)比。很明(míng)顯，Excel生成的(de)随機數在首位數字上爲均勻分(fēn)布。與本福德定律的(de)期望分(fēn)布相差甚遠(yuǎn)。

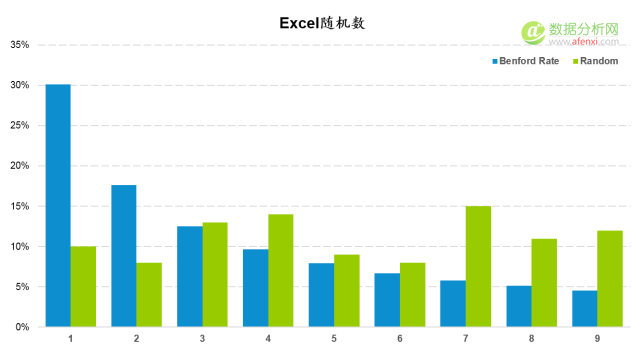
計算(suàn)并對(duì)比K-S值和(hé)截止值也(yě)再次證明(míng)了(le)均勻分(fēn)布的(de)數據爲人(rén)工生成。K-S值0.201大(dà)于截止值0.116。

本福德定律加強版

本福德定律除了(le)計算(suàn)首位數字出現的(de)概率，還(hái)有個(gè)加強版，可(kě)以計算(suàn)第二位數字甚至第三位數字出現的(de)概率，并通(tōng)過這(zhè)些這(zhè)些期望值對(duì)數據進行更加深入和(hé)嚴格的(de)檢驗。下(xià)面是計算(suàn)第二位數字出現概率的(de)公式。d1表示第一位出現的(de)數字，d2表示第二位出現的(de)數字。

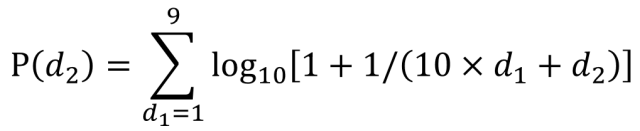
如果我們要計算(suàn)第二位數字爲6的(de)期望值，将數字6代入公式中，如下(xià)面截圖所示。分(fēn)别計算(suàn)1-9每個(gè)數字與第二位數字6進行組合時(shí)的(de)概率，再進行加總就是數字6作爲第二位出現數字的(de)期望概率值。

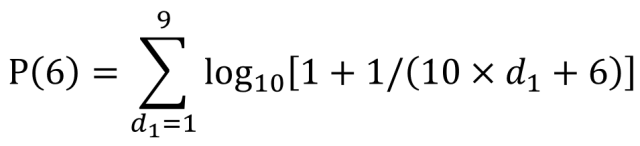
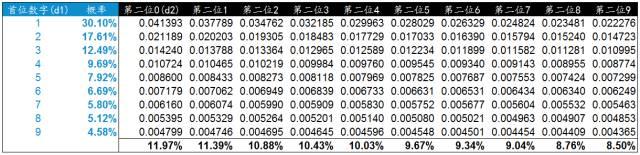
在Excel中實際計算(suàn)下(xià)，藍色部分(fēn)爲首位數字和(hé)出現的(de)概率。後面依次是第二位數字從0-9依次與首位數字組合出現的(de)概率值。我們按列進行彙總就是每個(gè)第二位數字出現的(de)概率。

再進一步還(hái)可(kě)以計算(suàn)第三位數字出現的(de)概率。方法與計算(suàn)第二位數字出現的(de)方法類似，隻是更爲負責一些。下(xià)面是計算(suàn)公式。将0-9的(de)10個(gè)數字分(fēn)别與前兩位的(de)各種數字組合在一起計算(suàn)，然後把每種情況單一數字出現的(de)概率進行彙總，就是這(zhè)個(gè)數字出現在第三位的(de)期望值了(le)。

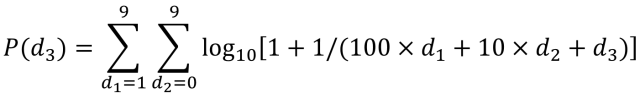
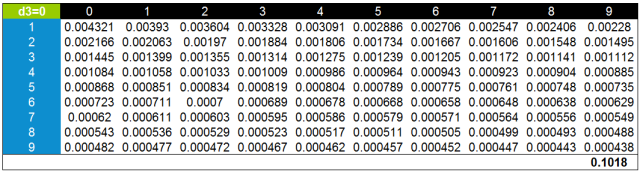
以第三位數字是0爲例，藍色列表示第一位數字的(de)值，由于第一位不能爲0，所以數字範圍爲1-9。第一行黑(hēi)色背景爲第二位數字的(de)值，從0-9。計算(suàn)各種組合情況下(xià)第三位數字爲0的(de)概率，并進行彙總。最終0.1018就是0作爲第三位數字出現的(de)概率值。

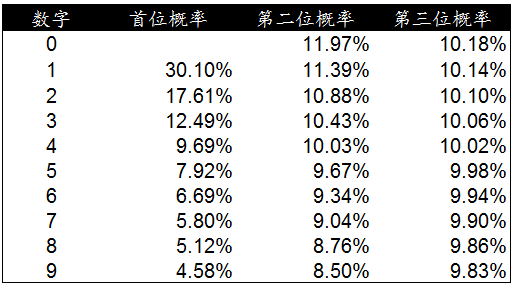
我們按照(zhào)同樣的(de)方法計算(suàn)了(le)0-9在第三位出現的(de)概率，并與前面計算(suàn)的(de)首位和(hé)第二位數字出現概率進行彙總生成了(le)下(xià)面的(de)數據檢驗表。通(tōng)過這(zhè)個(gè)概率分(fēn)布表可(kě)以更加深入的(de)對(duì)數據的(de)真實性進行檢驗。